Program for PDA capable of recognizing the language w#wR where w ∈ {0, 1}* and ∑={0, 1, #}
Formal definition of pushdown automaton (PDA)
A pushdown automaton is a 6-tuple (Q, Σ, Γ, δ, q0, F), where Q, Σ, Γ, and F are all finite sets, and
1. Q is the set of states,
2. Σ is the input alphabet,
3. Γ is the stack alphabet,
4. δ : Q × Σε × Γε→P(Q × Γε) is the transition function,
5. q0 ∈ Q is the start state, and
6. F ⊆ Q is the set of accept states.
- Alphabets Σε=∑ U {ε} and Γε=Γ U {ε}
- P( ) accounts for the non-determinism
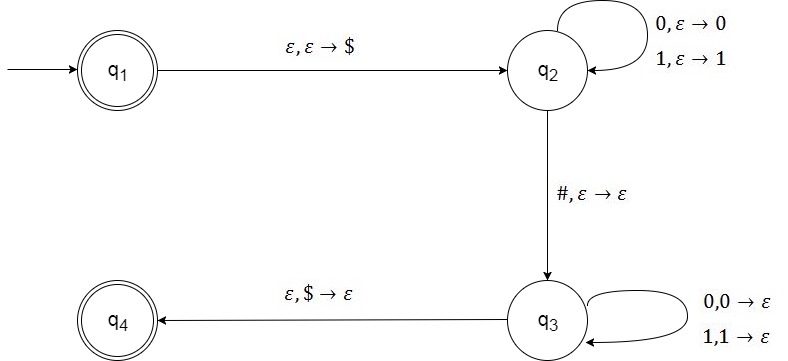
State Diagram
Here,
P = (Q, Σ, Γ, δ, q0, F), where
- Q = {q1, q2, q3, q4},
- ∑ = {0, 1, #},
- Γ= {0, 1, $},
- qs= q1
- F = {q1, q4},
δ is given by the following transition table, cell entries are new state and TOS symbol pair, blank entries are ∅.
Inputs are current state, input string and TOS symbols. Cell entries are new state and TOS symbol pair. Blank entries are ∅.
Transition Table:
Program
#include<stdio.h>
#define EOS '\0'
#define SIZE 101
char Stck[SIZE];
int top=-1;
void push(char symb)
{
Stck[++top]= symb;
}
char pop(void)
{
return Stck[top--];
}
int main()
{
char c,inpstr[SIZE];
int q,i;
scanf("%s",inpstr);
printf("\n");
printf("%s ",inpstr);
q=1;
i=0;
c=inpstr[i];
while(true)
{
if(q==1)
{
q=2;
push('$');
}
if(q==2)
{
if(c=='0')
{
q=2;
push(c);
}
else if(c=='1')
{
q=2;
push(c);
}
else if(c=='#')
{
q=3;
}
else
{
q=5;
break;
}
}
else if(q==3)
{
if(c=='0' && Stck[top]=='0')
{
q=3;
pop();
}
else if(c=='1' && Stck[top]=='1')
{
q=3;
pop();
}
else if(c==EOS && Stck[top]=='$')
{
q=4;
break;
}
else
{
q=5;
break;
}
}
else
{
q=5;
break;
}
i++;
c=inpstr[i];
}
if(q==5)
printf(" Rejected");
if(q==4)
printf(" Accepted");
printf("\n");
return 0;
}
I/O:
Input: 101011#110101
Output: Accepted
Input: 1010#1010
Output: Rejected
Input: 11#00
Output: Rejected


Comments
Post a Comment